データのばらつき度合いを見るときに「箱ひげ図」というグラフを使います。「箱ひげ図」は「中央値」や「四分位数」といった統計的指標の確認に適しています。
聞きなじみがなく、また、読み解くのが難しそうなこのグラフ、ルールさえ覚えてしまえば簡単に理解できます。また、Excelの標準機能範囲内でグラフの作成もできるのです。
この記事では、「箱ひげ図」の見方からExcelでの作り方まで図表を用いてわかりやすく解説します。
箱ひげ図はデータのばらつき具合を把握するのに役立つ
たとえば、「ある学校における1学期のテストの成績」をクラスごとに表現したいケースを思い浮かべてみてください。
アウトプットとしての箱ひげ図は次のようになります。
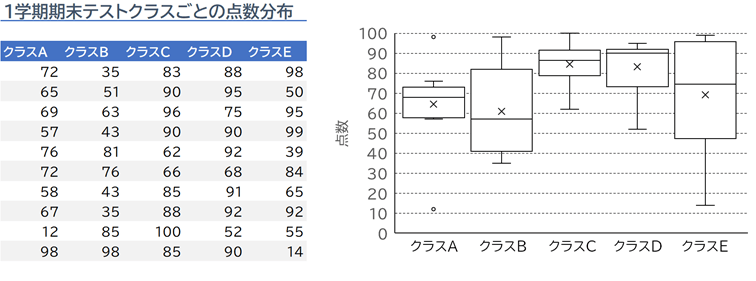
箱ひげ図は見慣れないという方も少なくないでしょう。
上図で示した箱ひげ図なるものを見ても、どんなデータに基づいて、何が示されているのかワケが分からないと感じるかもしれません。
図の左側に示した表と照らし合わせると、クラスの平均点が高いとグラフが上の方に示されていたり、クラス内の点数のばらつきが大きいと四角形の面積が大きかったりと、ぼんやりと特徴を掴めるかもしれません。
四角い箱の上下にひげをつけたグラフを「箱ひげ図」と呼びます。
箱ひげ図は、データのばらつきの度合いを表す際によく使われます。
もう少しだけ詳しく説明します。
箱ひげ図とは、長方形の「箱」と「ひげ」と呼ばれる直線で構成される図です。値の大きなデータから小さいデータまでを順に並べたときの分布を表しています。
「ひげ」の上端は最大値、下端は最小値を示しています。最大値と最小値の間に、全データを4分の1ずつ(つまり25%ずつ)収納できるよう、4つの区間に分けています(上図の場合、4つの横線で分割されている)。
・・・と言葉だけの説明では分かりにくいと思いますので、ここから図解を織り交ぜながら解説を進めます。
データの平均とばらつき
箱ひげ図を理解するには、まず、「データの平均」と「データのばらつき」を理解する必要があります。
テストの点数は生徒ごとに違う点数になります。もしも生徒の理解度が全く同じ場合、ほぼ全員が同じ点数を取ることが予想されます。逆に、理解度がばらばらの場合は点数に開きが出てきます。完璧に全くの同じ理解度に生徒を揃えることは普通できないので、点数はばらついていきます。その度合いは、元からの生徒の実力や、指導する先生、または指導する教材にも左右されます。そのようなことから各クラスで平均点も点数のばらつきも差が出てきます。
これと同じようなことは、勉強だけではなく、スポーツの記録や、料理、店舗への毎日の来店者数、工場で出荷する商品の性能など、様々な分野で起きています。
箱ひげ図の見方、読み取り方
箱ひげ図では四分位というばらつきの尺度を使います。
データが100個ある場合、まずそのデータを大きい順に並べます。
すると1番上が「最大値」、一番下が「最小値」になります。
上から25個目を「第一四分位」、上から50個目を「第二四分位」(正確には50個目と51個目の真ん中の値)、上から75個目を「第三四分位」と呼びます。
データが200個であれば、50個、100個、150個目を第一四分位から第三四分位と呼びます。
第二四分位はちょうど真ん中のデータになるので「中央値」と呼びます。
この四分位を元にしたばらつき度合い表しているのが箱ひげ図です。
箱ひげ図には箱が2つあり、その上下の箱が合わされた箇所の値が中央値となります。そして上の箱の上側が第一四分位、下の箱の下側が第三四分位です。
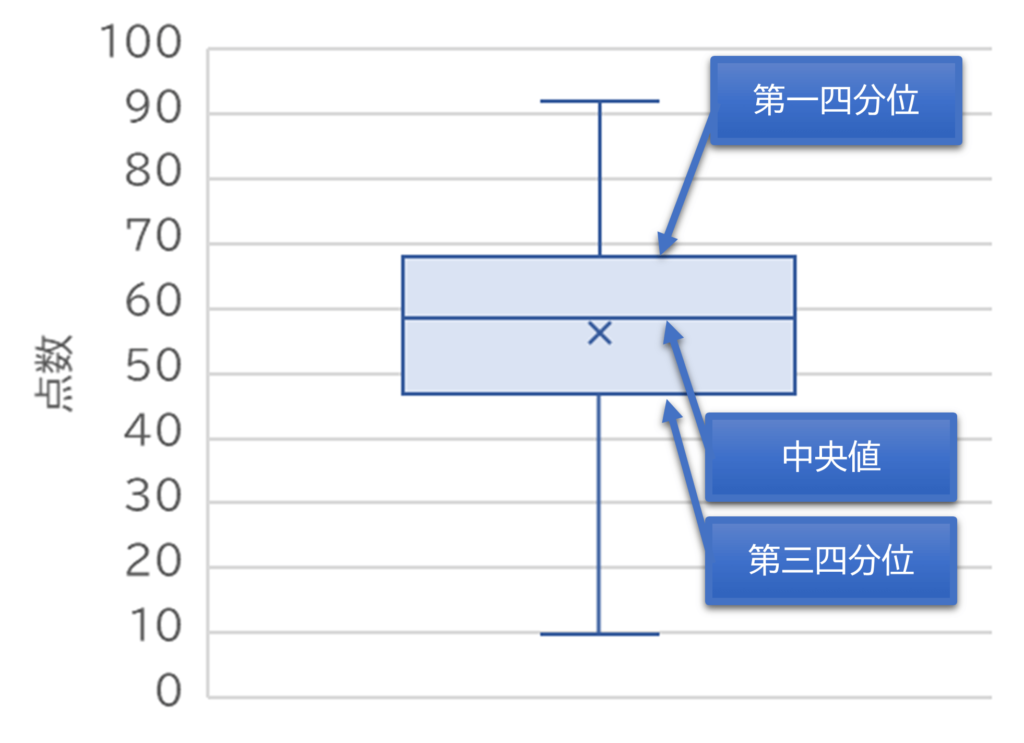
箱から線が上下に伸びています。これを「ひげ」と呼びます。
箱ひげ図のひげの表現の種類は2種類に分かれます。
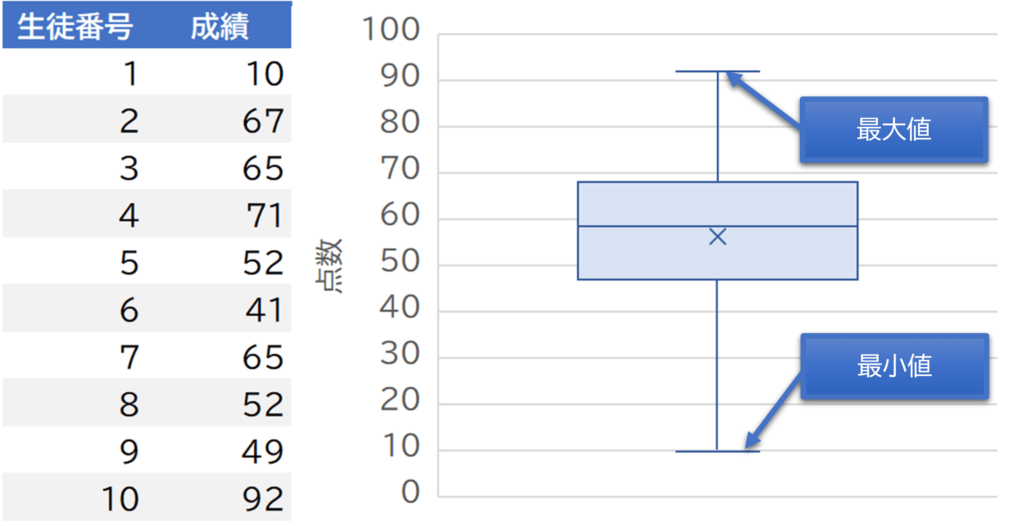
1つは上のひげの上側を最大値、下のひげの下側を最小値とするものです。この箱ひげ図であればデータが100個の場合は上から1つ目、25個目、50個目、75個目、100個目という並びなります。
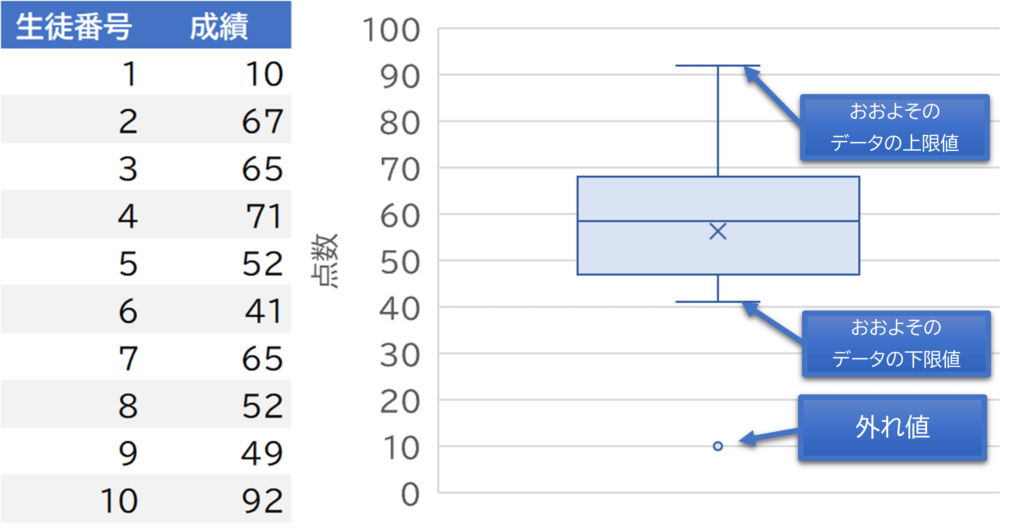
もうひとつは、まず第一四分位から第三四分位を差し引いた値を求めてそれを1.5倍します。第一四分位にその値を足してデータのうちその範囲にある最大値をおおよそのデータの上限とし、第三四分位からその値を引いてデータのうちその範囲にある最小値をおおよそのデータの下限とします。
おおよそのデータの上限を上のひげの上側とし、おおよそのデータの下限を下のひげの下側とするものです。
この場合の上下のひげの範囲に入っていないデータはデータの集まりの外にある値です。
このデータを「外れ値」と呼びます。
データが均等に並んでいる場合や一か所に集まっている場合は外れ値がないこともあります。その場合はひげの上下が最大値と最小値を表します。
箱ひげ図では外れ値があれば点を打って表現します。
また箱ひげ図ではデータの平均値は×で表現されています。
Excelで箱ひげ図を作成する方法・手順
Excel2016からは箱ひげ図をExcelで作成することができるようになりました。
手順は次のとおりです。
データ範囲を、項目を含めて選択します。
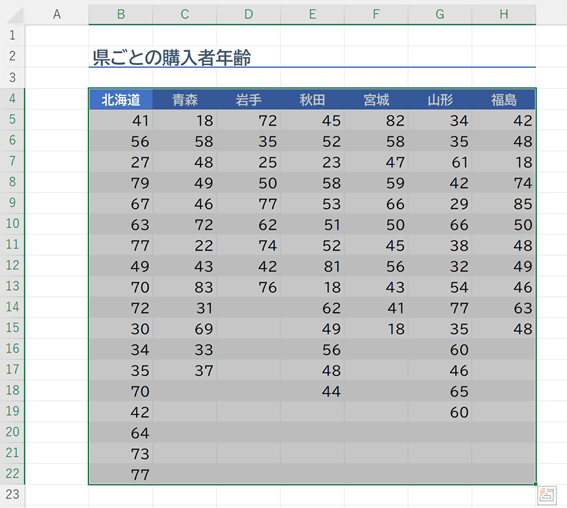
リボンの「挿入」タブの中の「グラフ」グループの「統計」グラフの中にある「箱ひげ図」をクリックします。
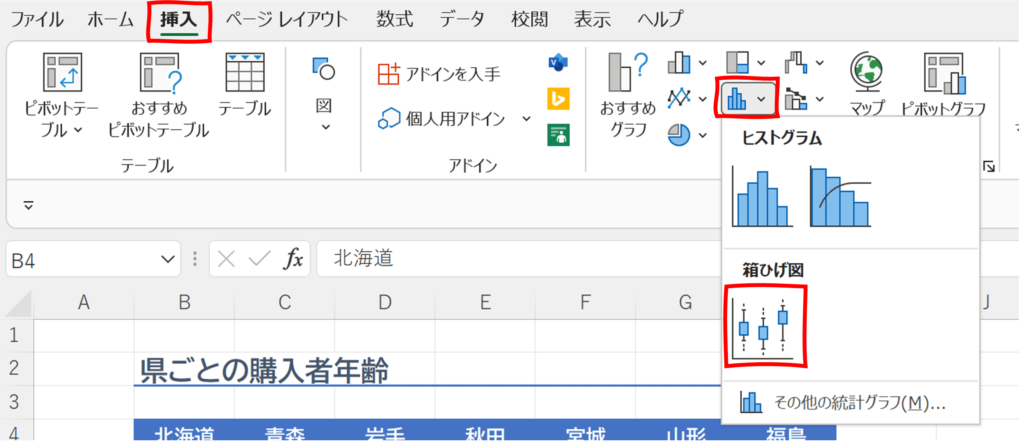
これだけで箱ひげ図が作成されます。
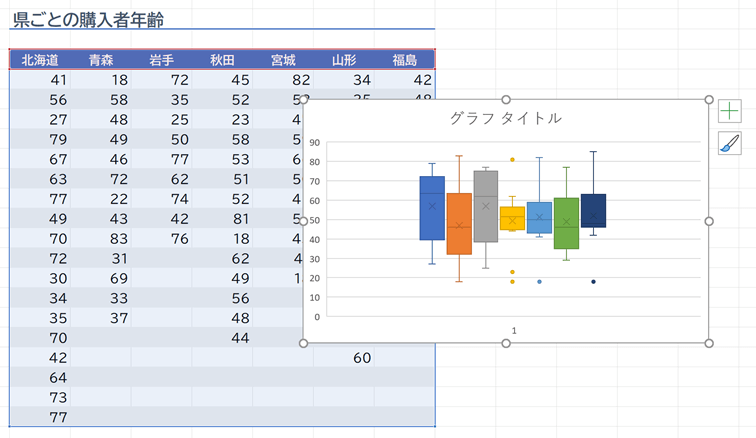
Excelで作成したグラフはグラフ四つ角の○をドラッグすることで大きさを変更でき、周りの線をドラッグすると位置を移動できますので、好きな大きさ、好きな位置に配置します。
Excelで作成した箱ひげ図はそのままでは、どれがどの項目かがわかりにくくなってしたったり、項目同士が近く中央に寄ってしまったりしています。少し改善してみましょう。
グラフの右上の「+」をクリックし、「凡例」の中の下をクリックします。
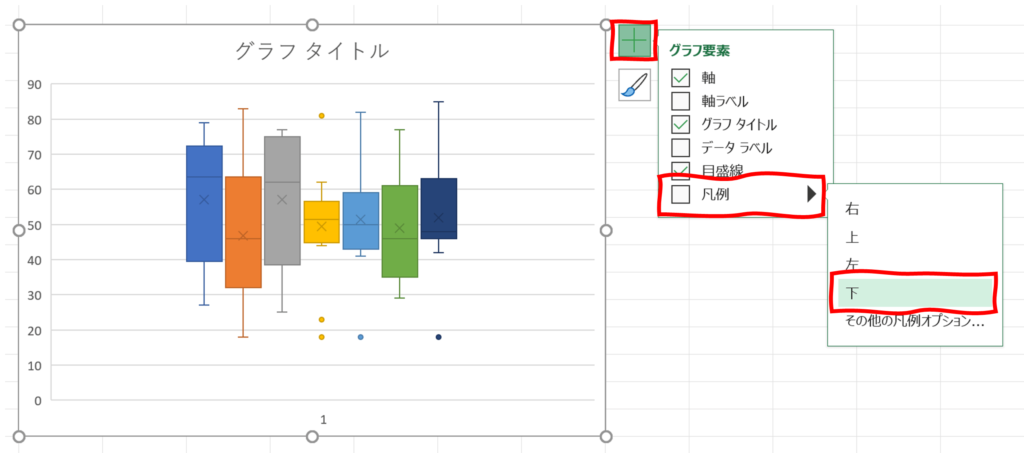
そうすることで、グラフの下側にどれがどの項目か表す凡例が表示されます。
また、グラフの下の方に「1」と言う文字が入っています。これは、横軸ですのでグラフの右上の+をクリックし、軸の第1横軸のチェックを外すことで消すことができます。
他にもグラフの右上の+でグラフタイトルの有無、第1縦軸のラベルの表示、非表示を切り替えることができるので適宜変更します。
次に、いずれかのグラフ要素を右クリックし、データ系列の書式設定をクリックします。
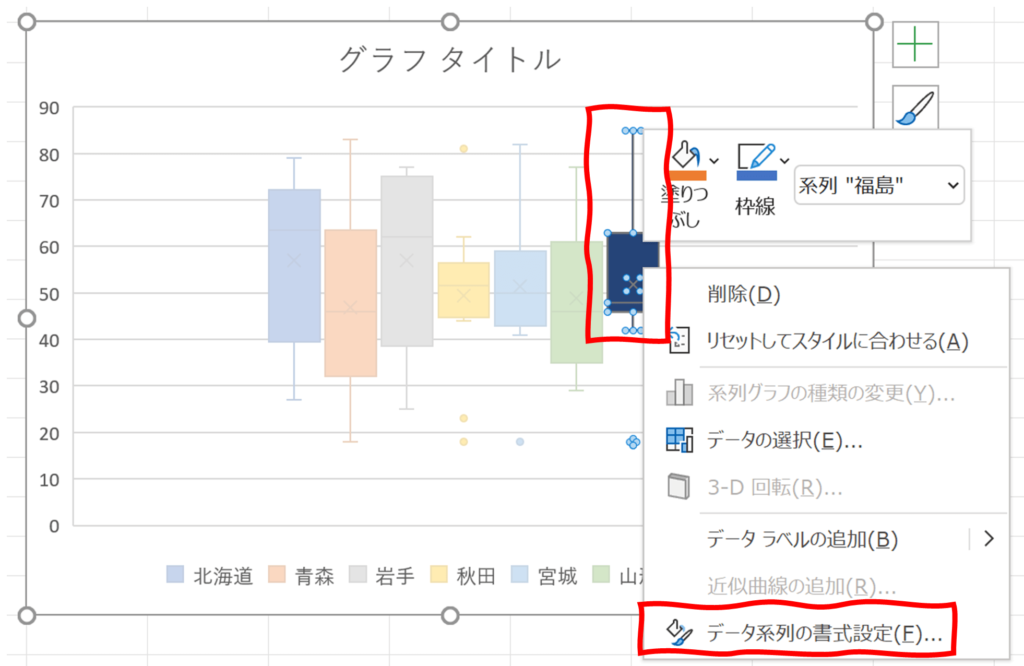
画面右側に表示されるデータ系列の書式設定作業ウィンドウのデータ要素の間隔を5%~10%程度に変更します。
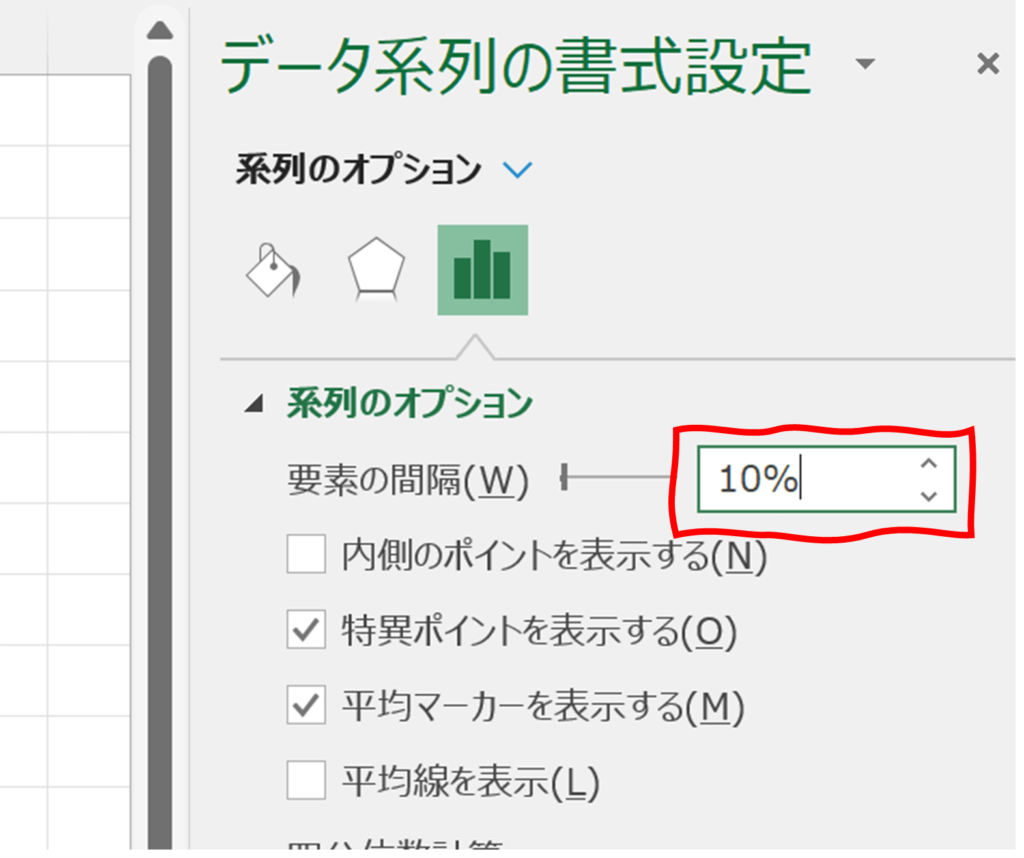
狭かったデータ系列の間隔が広がります。
以上のようにExcelでの箱ひげ図は若干クセがあり、見やすくするために修正が必要になるケースがあります。
箱ひげ図を使うメリット
データのばらつきを表す代表的なグラフはヒストグラムですが、ヒストグラムは1つのグラフに1つのデータしか描くことができません。
無理やり、複数の要素からなる上記の県ごとの購入者年を1つのヒストグラムで表現しようとすると次のようになり、どの県の傾向か一目では判断しにくくなります。また、調査人数がバラバラの場合も単純に比較ができなくなります。
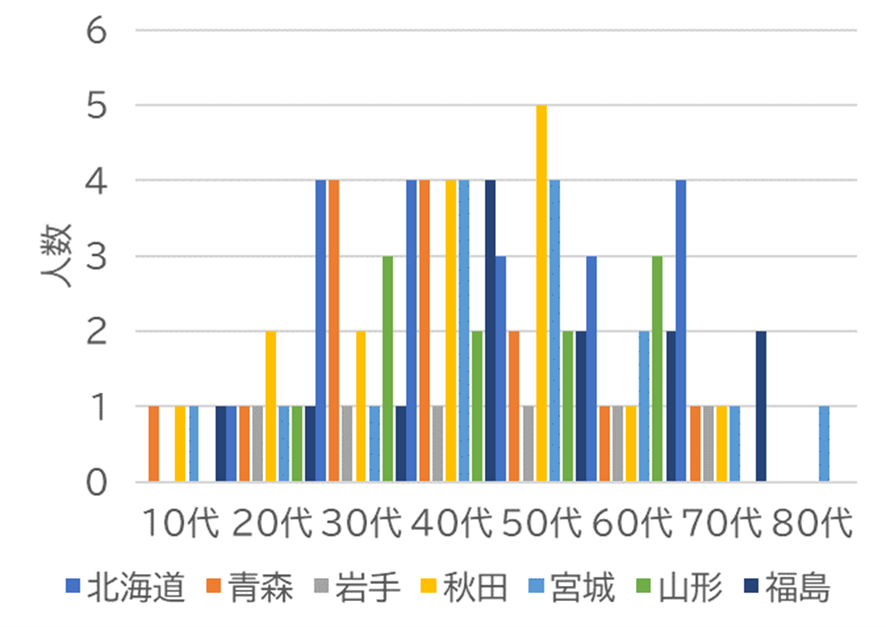
箱ひげ図では、1つのグラフに複数の要素のデータを描くことができるので、クラスごと、支店ごと、地域ごとなどが一度に比較できるという大きなメリットがあります。調査人数がバラバラでも、あくまで四分位を表現するので単純に比較が可能になります。また、外れ値を明確に表すことができるのもポイントです。
箱ひげ図を使う際の注意点
ヒストグラムで表したときに2つの山になるようなデータの場合、箱ひげ図ではうまく2つの山を表現することができないので注意が必要です。
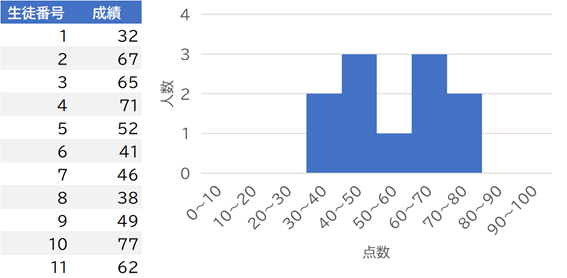
たとえば、次のデータをヒストグラムにすると40点台と60点台に2つの山が現れます。
2つの山があるということは、それぞれで別の要因が隠れている可能性もあり注意深く分析しなければならなくなります。
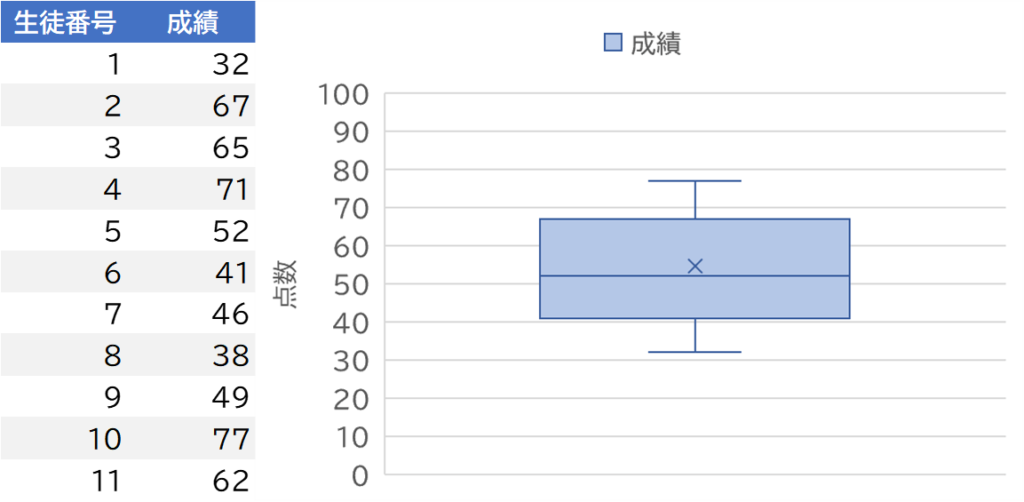
同じデータで箱ひげ図を描いてみた場合では、2つの山があるような傾向には見えなくなってしまいます。ここは注意すべき点です。
まとめ
この記事では、ばらつきの度合いを表現するグラフ「箱ひげ図」について解説しました。
特に複数の事柄のばらつき度合いを比較するためには便利なグラフです。中央値の線より上の箱の上の線までと下の箱の下の線までの距離を比べれば、上下どちらに向けてデータが広がっているかがわかります。上下のひげでデータ全体の広がりもわかります。また、箱ひげ図では外れ値を検出するにも便利です。
箱ひげ図を読み解くには、「四分位」という考え方を理解する必要がありました。四分位は箱ひげ図以外にもデータのばらつきの尺度として扱うことができる便利な考え方です。この記事の内容をよく確認しておきましょう。
Excelで箱ひげ図を描くことも簡単にできます。しかし、作ったそのままより、データ要素の間隔を整えたり凡例を追加したりしたほうが見た目がよいので、その操作方法も覚えておきましょう。


