2種類のデータのあいだの関係性の強さを表す「相関係数」という指標があります。
名前は聞いたことがあっても、その意味や計算方法については理解があいまいというケースが少なくありません。ビジネスシーンで相関分析をおこなう場合、「相関係数」を理解していなければ判断を誤ってしまう可能性があります。
この記事では、「相関係数」についてわかりやすく解説するとともに、Excelでの分析方法や相関係数を見るときの注意点もあわせてお伝えします。
相関とは?
相関とは、2種類のデータのあいだの関係性のことです。たとえば、気温が上がるとアイスクリームの売上が上がれば、売上も上がるようなケース。このように、片方が上がればもう片方も上がることを相関があると言います。
相関係数とは?重相関係数との違いは?
相関係数の意味
相関係数とは、2種類のデータのあいだにどのくらい関係性があるかを示す指標です。 別の言い方をすると、「線形的」つまり「直線的」な関係性を示す場合に用いられる指標で、相関係数の大小によって関係性の直線性を判断することができます。
グラフを見ると、より直感的に理解できるでしょう。下のグラフをご覧ください。2種類のデータのあいだに直線的な関係がある場合は「強い相関」があると言えますし、反対に直線的な関係が認められない場合は「弱い相関」「無相関」と言えます。
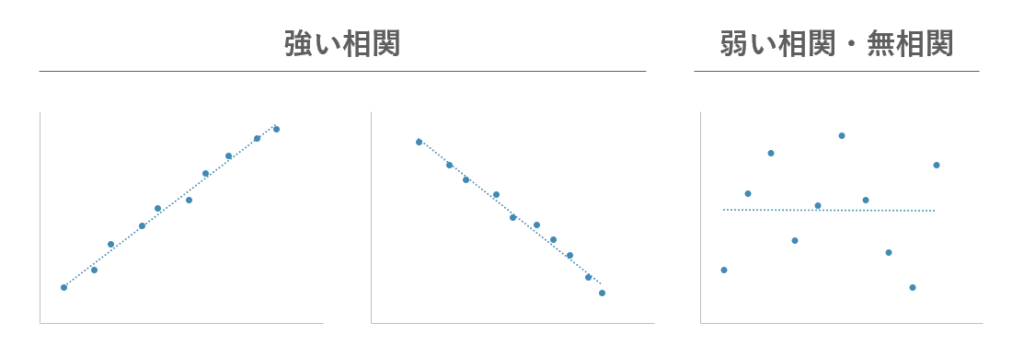
相関係数の範囲
相関係数は、-1から1までの値で表され、後述する「正の相関」が強いほどその値は1に近付きます。反対に、「負の相関」が強いほど-1に近付きます。なお、「無相関」の場合は、相関係数はゼロに近い値を示します。
重相関係数の意味
ちなみに、相関係数を2乗したものを重相関係数と呼びます。2乗するのでプラスマイナスは関係なくなります。
重相関係数の値によって、次のように区分けがされます。
- 1~0.7:強い相関がある
- 0.7~0.3:相関がある
- 0.3~0:相関なし
以下には、散布図とその散布図の重相関係数を示します。
- 重相関係数約0.7の散布図(=強い相関がある)
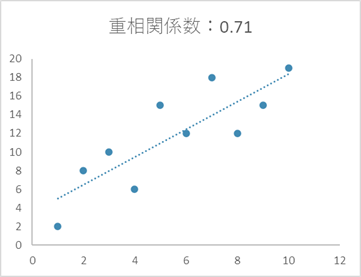
- 重相関係数約0.04の散布図(=相関がない)
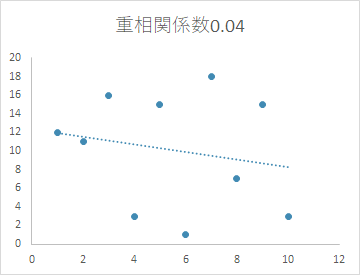
相関係数の計算方法
相関係数は一般的にrで表されます。相関係数rを求めるには、2種類のデータの共分散とそれぞれの標準偏差が必要です。

共分散は、2つのデータ同士を1つずつかけ合わせた値の平均から2つのデータの平均を引いたもので、正の相関の時に正の値になり、負の相関の時に負の値になるものです。無相関の場合は共分散も0になります。
標準偏差は、データの一つ一つをデータの平均値を差引いた値を2乗したものを合計した値の平方根となります。成績の偏差値を求める時に使う指標で有名な値ですね。
これらの定義をもとに、上記の式を分解すると次のような公式で示すことができます。

この公式を解くには複雑で、とても多くの労力を費やしますが、
ひとつひとつのデータを繰り返しかけ合わせたり、平均より差し引いたりすることで標準偏差や共分散を求め、それらを使うことで相関係数が求められる
というポイントを理解しておけば十分です。
Excelで相関係数を算出する方法
ExcelのCORREL関数を使う|2種類のデータ間の相関係数を算出する場合
実は、複雑な計算をしなくても、Excelを使えば相関係数を求めることが可能です。2つのデータの集まりがあれば、それらの間の相関係数をCORREL関数で求めることができます。
CORREL関数は次のように使います。
=CORREL(1つ目のデータの集まり,2つ目のデータの集まり)セルB2からB13までに1年間の月ごとの宣伝費、C2からC13までに売上を入力した表の場合、宣伝費と売上の相関係数を求めるには、次の計算式になります。
=CORREL(B2:B12,C2,C12)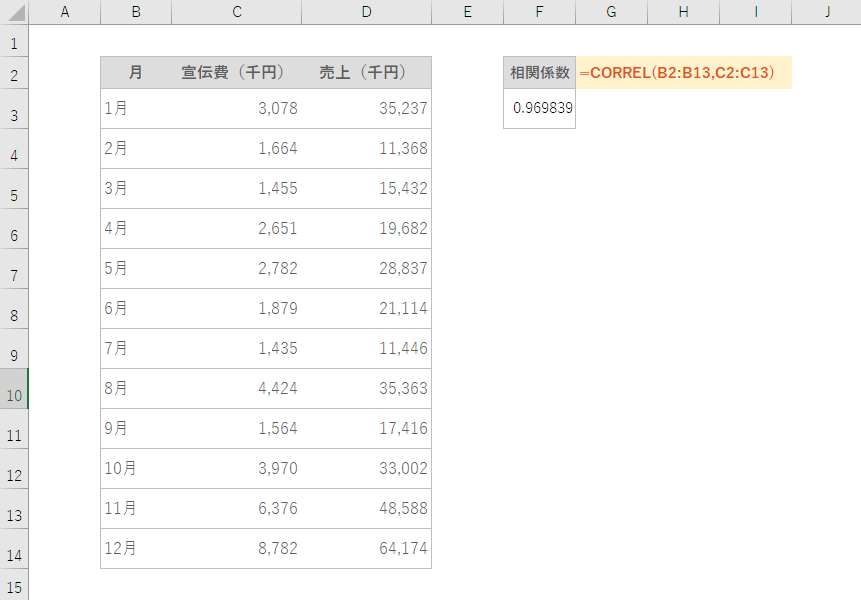
重相関係数を求める場合は、この計算式に2乗すればいいので、次の計算式になります。
=CORREL(B2:B12,C2,C12)^2Excelの分析ツールを使う|3種類以上のデータの中から、2種類をピックアップして相関係数を算出する場合
CORREL関数を使えばすぐに相関係数を算出できて便利なのですが、比較したいデータの種類が3種類以上になると、ひとつひとつ計算しなければならないため若干面倒です。
そんなときに便利なのが、Excelの分析ツールです。
Excelの分析ツールは、初期設定では非表示になっているので設定が必要です。以下の手順で機能をONにしましょう。
- 画面上部のファイルタブをクリックする
- 画面左下のオプションをクリックする
- Excelのオプション画面が起動するので、画面左下のアドインをクリックする
- 同画面の下部に、管理「Excelアドイン」というメニューがあるので、その右側の設定ボタンをクリックする
- 有効なアドインの中にある「分析ツール」にチェックを入れ、OKボタンをクリックする
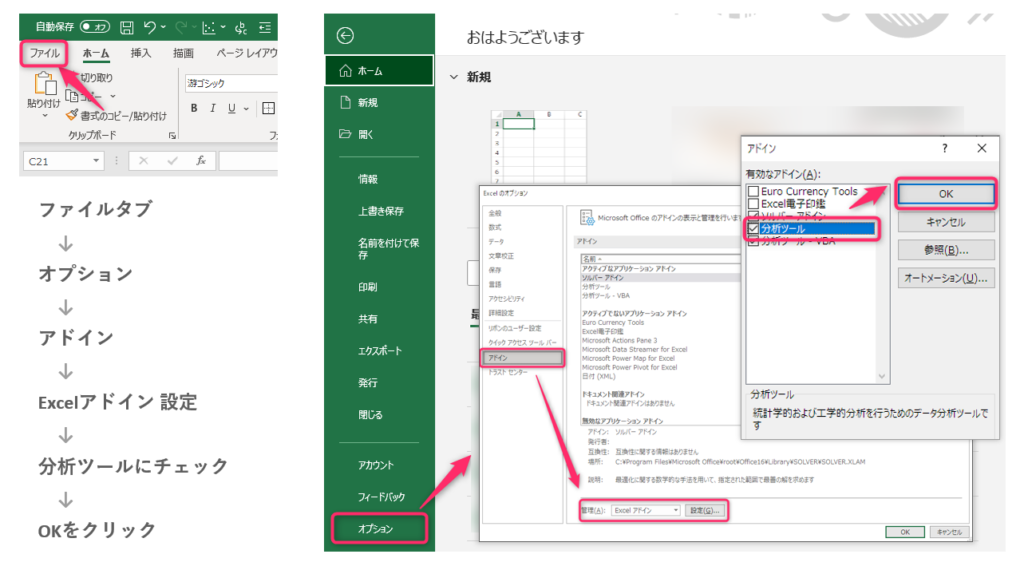
ここまで完了したら、画面上部のデータタブをクリックしましょう。画面右上に「分析ツール」が表示されていたら設定は完了です。

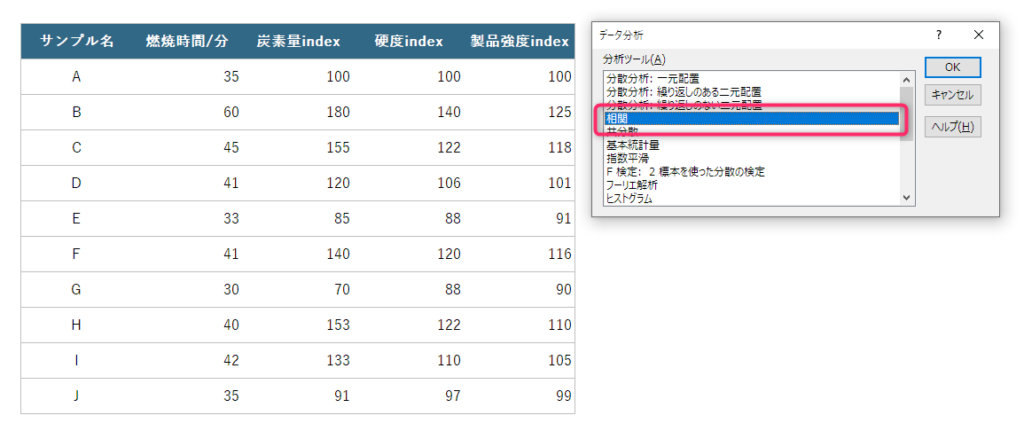
データを準備したら、上記の「分析ツール」をクリックすると、分析ツール画面が立ち上がります。メニューの中から「相関」を選択し、OKボタンを押下しましょう。
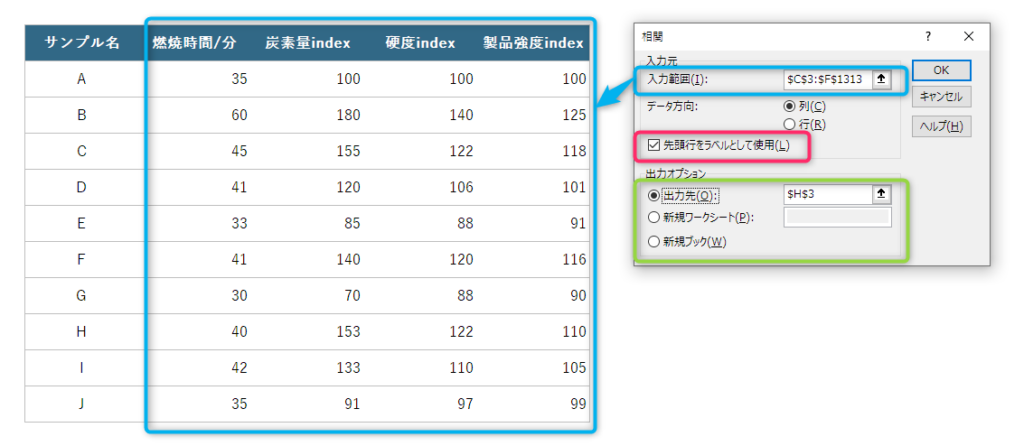
「入力範囲」には、分析対象のデータを指定します(下図水色部)。このとき、列の項目名も含めて分析対象データを指定しておくことをおすすめします。なぜなら、分析結果を見るとき読みやすくなるためです。
列の項目名を含んだ場合は、必ず「先頭行をラベルとして使用」にチェックを入れましょう(下図ピンク部)。
最後に、出力先を指定します(下図黄緑部)。好きな場所に結果をアウトプットすることができます。今回はわかりやすさのために、元データの隣に結果を表示します。
OKボタンを押下すると、以下のとおり結果が出力されます。
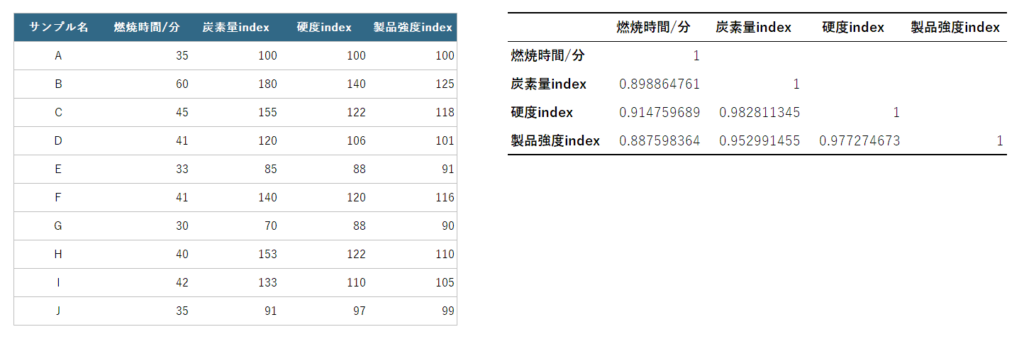
表の縦と横に記載されたデータが交差する箇所に、相関係数が表示されているのがわかります。たとえば、燃焼時間と炭素量の相関係数はおよそ0.899です。
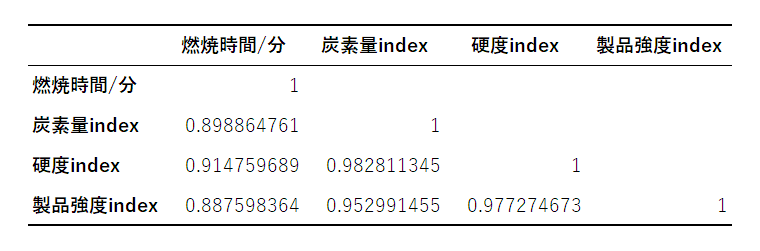
以上のように、Excelの機能を使うだけで簡単に相関係数を求めることができるのです。
相関は3種類に分類できる
相関係数の値をもとに、相関は3種類に分類することができます。
- 正の相関: 相関係数が1に近い値を示す場合
- 負の相関: 相関係数が-1に近い値を示す場合
- 無相関: 相関係数がゼロに近い値を示す場合
相関関係は、散布図というグラフ(X軸/Y軸からなるグラフ上に、2種類のデータをプロットしたもの)で表すことができます。以下では、サンプルデータと散布図を用いて、3つの相関について解説します。
正の相関:相関係数が1に近い値を示す
正の相関とは、「2種類のデータのうち、一方のデータの値が大きいほど、他方のデータの値も大きくなる」という関係性を指す言葉です。
たとえば、ある市の間取り3LDKのマンションについて、物件ごとの床面積と販売価格をプロットすると、下図のような関係性が見られたと仮定します。図によると、床面積が広くなるほど販売価格が高くなるという関係が認められます。これらのデータのあいだには「正の相関」があると言えます。
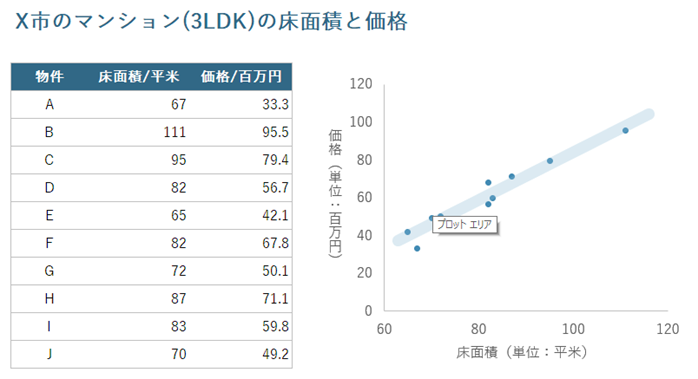
負の相関:相関係数が-1に近い値を示す
負の相関とは、「2種類のデータのうち、一方のデータの値が大きいほど、他方のデータの値が小さくなる」という関係性を示す言葉です。
たとえば、タイピングの練習時間とタイピング課題を終えるのにかかるタイムをプロットすると、練習量を増やせばタイムは縮む関係が認められ、図のように「負の相関」があると言えます。
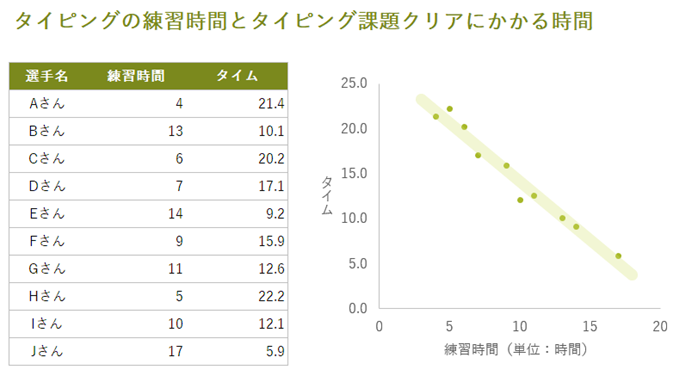
無相関:相関係数がゼロに近い値を示す
無相関とは、「2種類のデータのうち、一方のデータの値が大きくなっても、それに応じるかたちで値の増減が起きない」という関係性を指す言葉です。
たとえば、社員が1日にかける食事時間の月間平均値のデータと、彼ら・彼女らの昇格試験における得点をプロットしたとします。両者の間には何の関係性も見いだせないため、こういったケースは「無相関」と言えます。
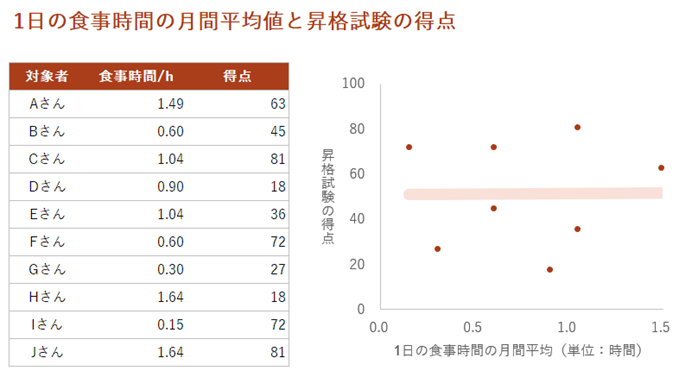
相関係数がゼロに近い場合には注意が必要
相関係数は「線形的」、つまり「直線的」な関係性を示す場合に用いられる指標です。言い換えると、「非線形的」な関係性は適切に評価しにくい指標です。
以下の例をご覧ください。
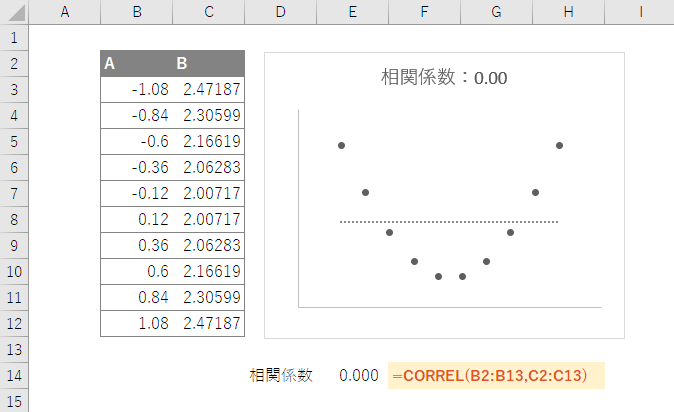
この場合、相関係数rの値はゼロですが、グラフを見る限り2種類のデータの間に関係性がないとは言い難いでしょう。相関係数rだけを見て判断すると、現象を見誤ってしまいかねません。この点に注意してデータを見る必要があります。
コラム|アンスコムの例(Anscombe's Quartet)
散布図が違っていても、相関係数などの統計量が同じになる現象のことを、アンスコムの例(アンスコムの数値例、Anscombe's quartet)といいます。
アンスコムの例は、以下のグラフに示された4つのデータセットで構成されており、4つのデータすべてにおいて相関係数などの統計量が同一の値を示すのです。
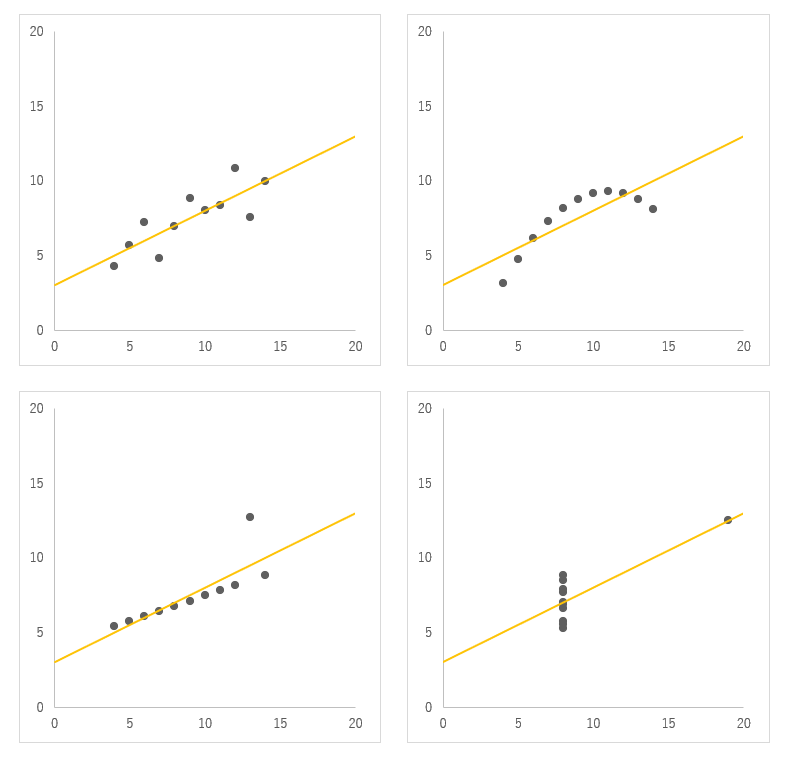
アンスコムの例において同一になる統計量は以下のとおりです。
| 統計量 | 統計量の値 |
|---|---|
| x の平均 | 9 |
| x の分散 | 11 |
| y の平均 | 7.50 |
| y の分散 | 4.122 or 4.127 |
| 相関係数 | 0.816 |
| 回帰直線 | y = 3.00 + 0.500x |
相関係数だけに着目してしまうと、どのデータセットも同程度の相関の強さを有するように見えますが、実際には全く異なる現象を示すデータセットであることが見て取れるでしょう。
データを見るときは、基本統計量などの数値情報だけに着目するのではなく、散布図など可視化したかたちでもデータを把握する必要があります。
相関係数を求めるときのポイント、注意点
相関係数を算出することで、今まで直感的に「これとこれは関係があるのではないか」と思っていたものが、関係があるかどうかを定量的かつ具体的に検証することができます。
スーパーマーケットのレジ係が店長に「牛乳を買う人はパスタも買うことが多い気がします」と報告するシーンを想像してみてください。
実際のレジのデータを分析して相関係数を算出し、相関関係があると判断できれば、牛乳とパスタを一緒に買う人には「牛乳を使ったパスタのレシピを配る」などの打ち手を考えることができるようになります。
そのほかにも、以下のような応用も可能でしょう。
- 農業:日照時間、肥料の量と作物の生育状況
- 産業:燃料に使われている添加物の量と車の燃費
- 商業:パンフレットの発行数、商品の販売数
- 災害対策:降雨量と災害の規模
相関係数や重相関係数の算出を通じて、データ間に強い相関が認められれば、高い精度でデータを予測することができます。データの予測には「回帰分析」という手法を用います。
相関係数は、手作業で探すと手間がかかるので、Excelや統計解析ソフトを使うと簡単に見つけることができます。今回はExcelのCORREL関数を使いましたが、関数電卓や各種ツール、プログラミング言語を用いて算出することも可能です。
相関係数は、あくまでも関係の強さを表すものです。よく勘違いされるケースとして、2種類のデータから構成される散布図の傾きが大きいほど、相関係数が高いと思われることがあります。しかし、これは誤りです。相関係数は、係数が大きいほど予測の精度が高いという性質を持っています。
相関関係には、因果に基づく相関関係と、別の要因によって引き起こされる相関関係があります。
気温とアイスクリームの売り上げには正の相関があり、気温とおでんの売り上げには負の相関があります。両者をあわせると、アイスクリームとおでんの売り上げには負の相関があるように見えます。
しかし、これは温度という別の要因を介した相関関係であり、両者の間には因果はありません。このような相関関係を「疑似相関」と呼び、本来の意味での相関ではない点に注意が必要です。
同じように、販売個数と売上金額に着目すると正の相関があるのは想像に難くないでしょう。しかし、これも本来の意味での相関ではないですね。売上金額は、価格と販売個数の掛け算によって求められる値だからです。
計算上そうなるのは自然な関係なので、相関とは言えません。
まとめ|相関係数は相関分析の基礎!意味をしっかり理解しよう
相関係数とは、2種類のデータの関係性を定量的に示すことができる指標、とお伝えしてきました。直感的に理解できる便利な指標ですが、アンスコムの例のように外れ値の影響を大きく受けたり、同じ値であっても全く異なる現象を示したりすることがあるので注意が必要です。また、相関係数は、Excelの関数や解析ツールを使って簡単に計算できることもわかっていただけたのではないでしょうか。今後、相関分析を行う際には、ぜひ活用してください。



