シンプソンのパラドックスとは、
データをいくつかのグループに層別したとき、「グループごとに観察された相関関係が、データ全体でも同じように観察されるはずだ」という直感に反し、データ全体としては異なる相関を示すパラドックス
のことです。
…いきなり意味不明だと感じたかもしれません。
この記事では、シンプソンのパラドックスについて図解・事例を用いてわかりやすく解説していきますのでご安心ください。
最後まで読んでいただければ、データへの向き合い方が少し変わるかもしれませんよ。
シンプソンのパラドックスとは?
シンプソンのパラドックスの概要
シンプソンのパラドックスとは、簡単に言うと「グループやセグメントごとに見たときの相関と全体で見たときの相関が逆転する現象」のことです。
なお、パラドックスとは、直感に反する現象だと考えていただいて構いません。
言葉ではイメージしづらいと思うので、簡単な例を以下に示します。
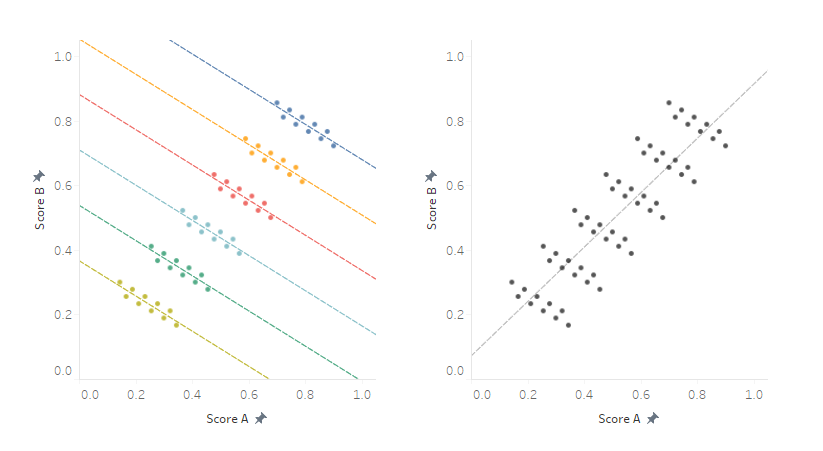
ある組織におけるScore AとScoreBの相関関係を散布図で表したものです。組織は6つの班に分かれているとしましょう。
上の図は以下のように読んでください。
- 左図:班ごとの結果が識別できるよう、6色で表している。
- 右図:組織全体の結果はを示している。グループ分けしていないので、単色で表している。
- 各散布図内の破線(---):傾向線。つまり、左図では班ごとの傾向、右図では組織全体の傾向を示している。
以上を踏まえると、班ごとの傾向(Score Aが高くなるほど、Score Bは低くなる)と全体の傾向(Score Aが高いほど、Score Bも高くなる)が異なることが見て取れるでしょう。
このような現象を、シンプソンのパラドックスと呼ぶのです。
▼相関関係については、以下の記事で解説しています。あわせてご覧ください。
シンプソンのパラドックスは誰の発見?
英語ではSimpson's paradoxと表現されることからわかるように、シンプソンさんが発見した現象というのは想像に難くないでしょう。
シンプソンのパラドックスは、統計学者エドワード・H・シンプソンが1951年に発表した論文で提唱した現象です。
Simpson, E.H. (1951), The Interpretation of Interaction in Contingency Tables. Journal of the Royal Statistical Society: Series B (Methodological), 13: 238-241. https://doi.org/10.1111/j.2517-6161.1951.tb00088.x
その後、同じく統計学者であるコリン・R・ブライスが1972年に発表した論文において「シンプソンのパラドックス」と命名しました。
実は、この現象を発見したのはシンプソンが初めてではありません。例えば、カール・ピアソンは1899年に、ウドニー・ユールは1903年に同様の現象を報告しています。
このような背景から、シンプソンのパラドックスは「ユール=シンプソン効果」と呼ばれることもあるのです。
シンプソンのパラドックスの具体例3選
シンプソンは論文において「トランプの柄×トランプの汚れ」と「治療有無×生存率」の事例を挙げてパラドックスについて説明しています。
事例1:トランプの事例
トランプは全部で52枚あります。そのうち、赤色のものが26枚、黒色のものが26枚あり、赤黒それぞれ20枚の数字(1~10のカード|Plain)と6枚の絵柄(Jack、Queen、King|Court)で構成されています。
これら一組のトランプの中に、汚れたもの(Dirty)ときれいなもの(Clean)があるケースを想像してみてください。
DirtyとCleanが下図のような割合で存在する状況です。
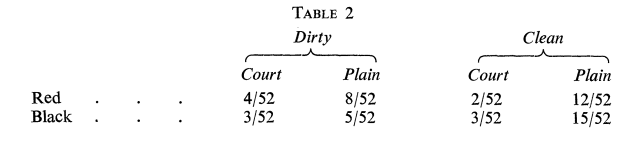
図示すると以下のようなイメージですね。
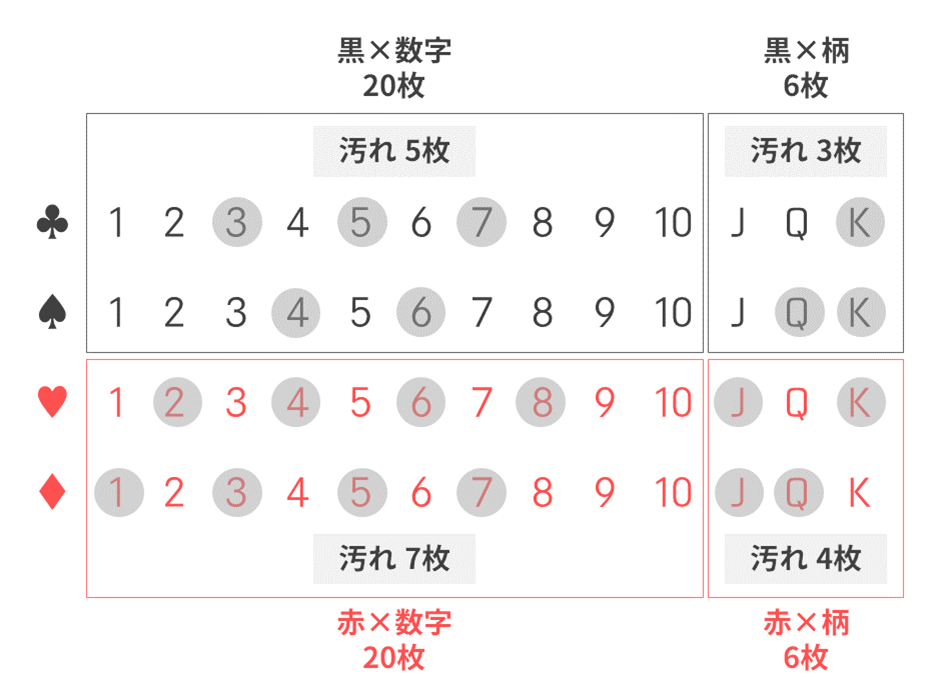
Dirtyなカードの場合、赤色はCourt(絵柄)の中に約57%、Plain(数字)の中に約62%含まれています。
一方で、Cleanなカードの場合は、赤色はCourtの中に40%、Plainの中に約44%含まれています。
こう見ると、赤色が偏在しているように見えます。しかし、全体で見るとどうでしょう?

当然ながら、赤色はCourtの中に50%、Cleanの中に50%含まれます。
この現象から得られる示唆は、「なんらかのグループ分けをして見たときの傾向と、全体で見たときの傾向は異なる可能性がある」ということ。
事例2:治療と生存率の事例
次に、治療の有無と生存率との関係性を、男性・女性にグループ分けして調査した結果を示します。
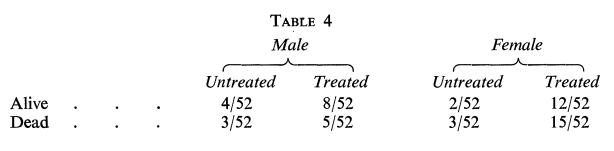
こちらも先ほどと同様に図示してみましょう。以下のようなイメージです。
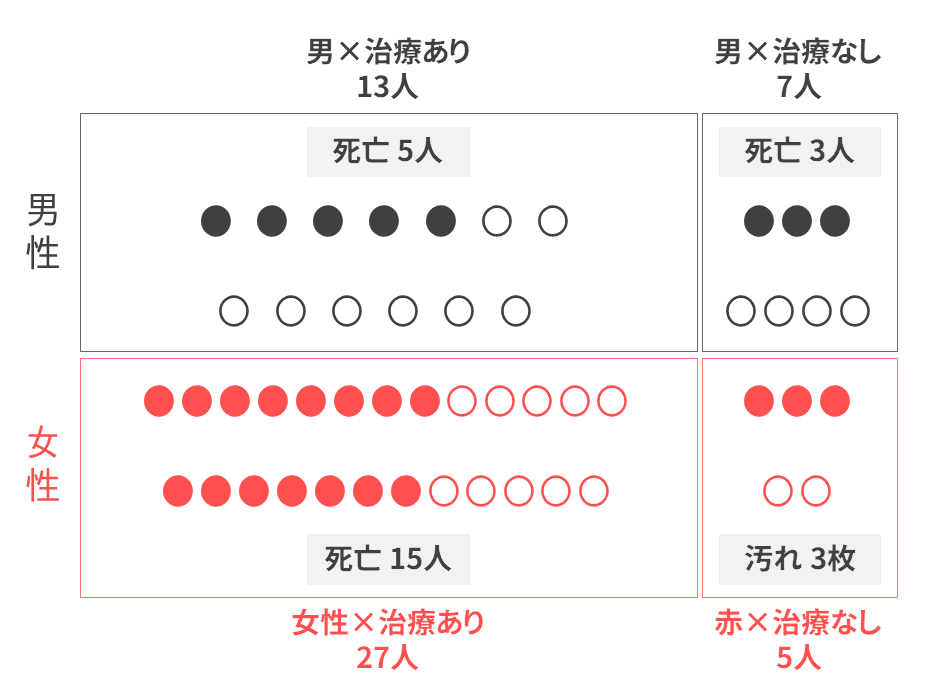
男性だけで見ると、治療ありの方が治療なしよりも生存率が高いです(治療あり:約62% > 治療なし:約57%)。
女性の場合も、治療ありの方が治療なしよりも生存率が高いです(治療あり:約44% > 治療なし:40%)
少し整理してみましょう。全体で見るとどうでしょう…?
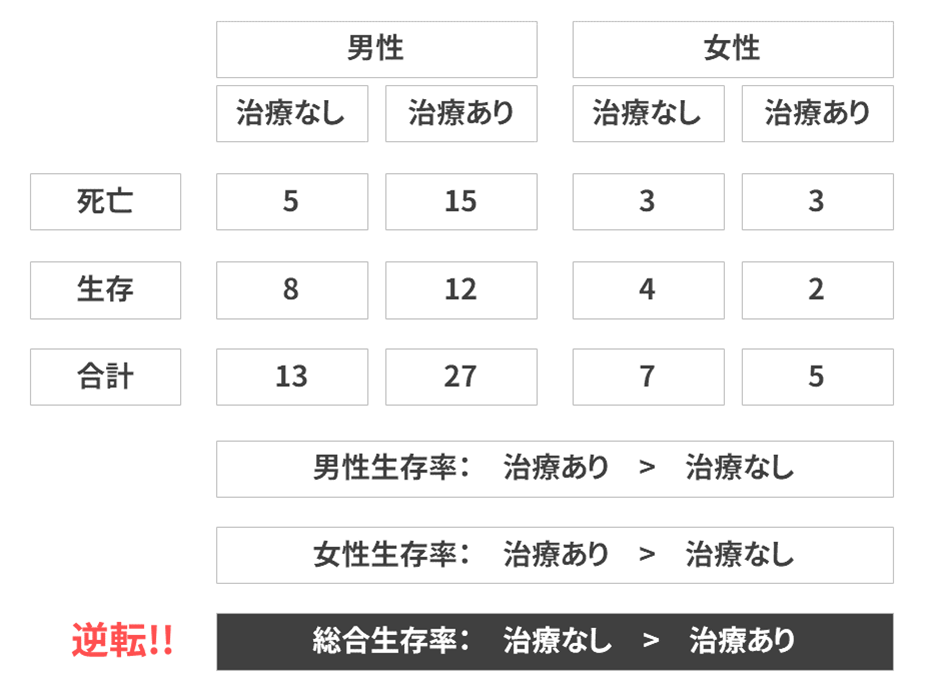
男女の区別なく、治療有無による生存率を算出すると、治療なし:60% > 治療あり:約44%と逆転現象が起きるのです。
男性、女性とグループ分けしたときには治療が生存に寄与するのに、全体でみると寄与しない。これがパラドックスです。
以上より、同じデータセットであっても、「もっともらしい解釈(sensible interpretation)」を導き出す分析方法は、ケースバイケースで異なる、という示唆が得られます。
事例3:新型コロナウイルス(COVID-19)のワクチンが重症化に及ぼす影響
COVID-19ワクチンの重症化予防効果に関する統計において、シンプソンのパラドックスが観測される例をご紹介します。
Israeli data: How can efficacy vs. severe disease be strong when 60% of hospitalized are vaccinated?
https://www.covid-datascience.com/post/israeli-data-how-can-efficacy-vs-severe-disease-be-strong-when-60-of-hospitalized-are-vaccinated
かいつまんで言うと、「一見すると、このワクチンは重症化予防に効果がないように見えるが、年齢で層別化すると効果があることがわかる」という内容です。
重症化の人数を見ると、ワクチンの接種有無で重症化抑制効果は変わらない=ワクチンの効果はない、という結果に見えます。
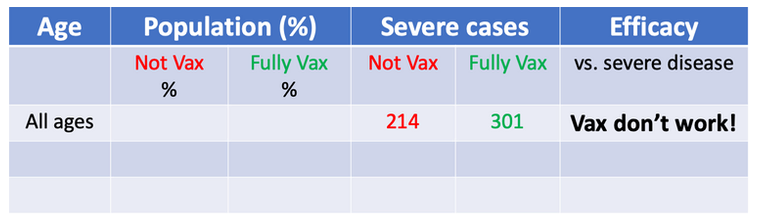
しかし、この結果には全体の人数が書かれていませんね。全体の人数を入力すると見え方が変わります。ワクチン接種者の方が全体の人数が多いため、重症化率という観点ではワクチン接種の効果が見られます。
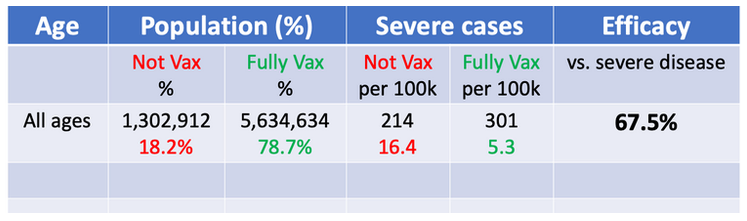
さらに、年代で層別したときは以下のような結果になります。
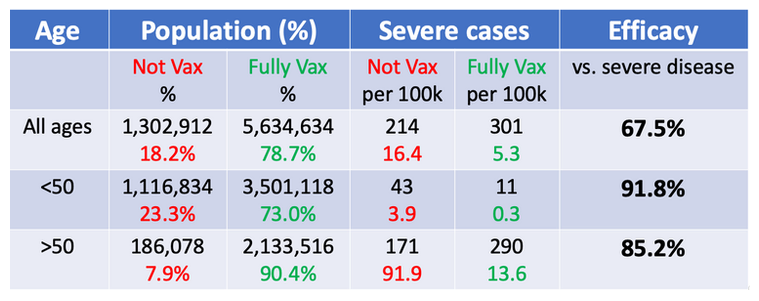
つまり、50歳よりも高齢の場合、ワクチン接種有無による重症化率へのインパクトは大きいことが分かります。
まとめ
データセットを分割する場合、サンプル全体の相関と各グループにおける相関のあいだにズレが生じる可能性がある、ということを念頭に置いてデータに向き合う必要があるでしょう。交絡因子を適切に調整することによって解消することができるバイアスと捉えることもできますが、データだけで因果関係を判断できると過信しすぎないことをオススメします。


